YOLO源码学习过程-YOLOv2（一）

学习YOLOv2源码（一）

​ 记录学习YOLOv2论文，原理以及阅读理解代码过程。

​ 至于为什么不从YOLOv1开始学习呢，是因为学习YOLOv1的时候，本博客还没建立，所以没有系统的写笔记，也懒得重新写了，哈哈。

论文地址：[1612.08242] YOLO9000: Better, Faster, Stronger (arxiv.org)

项目主页：YOLO: Real-Time Object Detection (pjreddie.com)

1.Batch Normalization 的基本原理

​ Batch Normalization（BN）层通过标准化每一层的输入（均值为 0，方差为 1），在训练阶段加速模型收敛、提升性能）、允许更高学习率、提供正则化效果（减少 Dropout 依赖）并增强稳定性，支持 YOLOv2 的多尺度训练和 Darknet-19 网络的高效训练；在测试阶段则退化为固定线性变换，确保推理一致性，整体上显著优化了模型的训练效率和检测精度。

​ BN 的核心思想是对每一层的输入进行标准化处理，使其均值为 0，方差为 1，然后再通过可学习的参数进行缩放和平移。具体步骤如下：

对于输入 $x$（比如卷积层的输出），BN 的计算过程是：

​ 1) 计算mini-batch 的均值和方差：

$$\begin{aligned}&\bullet\quad\text{均值:}\:\mu_B=\frac{1}{m}\sum_{i=1}^mx_i\\&\bullet\quad\text{方差:}\:\sigma_B^2=\frac{1}{m}\sum_{i=1}^m(x_i-\mu_B)^2\end{aligned}$$

​ 2）归一化：

$$\bullet\quad\hat{x}_i=\frac{x_i-\mu_B}{\sqrt{\sigma_B^2+\epsilon}}\quad(\epsilon\text{是小常数,避免除零})$$

​ 3）缩放和平移：

$$\begin{aligned}&\bullet\quad y_i=\gamma\hat{x}_i+\beta\\&\bullet\quad\text{这里 }\gamma\text{ (尺度参数)和 }\beta\text{ (偏移参数)是 BN 层的可学习参数}\end{aligned}$$

最终输出 $y_i$是对输入 $x_i$标准化后的结果，并且通过 $\gamma$ 和 $\beta$ 调整了分布。

​ 通常，BN层会放在卷积层后面，然而一般卷积层都会附带一个偏置参数：bias。然而，这个偏置参数会在在 BN 中被消掉，Why?

​ 在卷积层或全连接层中，通常的计算是：

$$z=Wx+b$$

其中，

$$\begin{aligned}&\bullet\quad W\text{ 是权重矩阵}\\&\bullet\quad x\text{ 是输入}\\&\bullet\quad b\text{ 是偏置项 (bias)}\end{aligned}$$

​ 当输出 $z$经过 BN 层时，会被标准化为均值 0、方差 1 的分布，然后再通过$\gamma$和 $\beta$ 调整。让我们分析一下 $b$ 的作用：

​ 1.BN 的均值减法抵消了 bias：

$$\begin{aligned}&\bullet\text{ 在 BN 的归一化步骤中,计算 }\hat{x}_i=\frac{z_i-\mu_B}{\sqrt{\sigma_B^2+\epsilon}}\\&\bullet\quad\text{假设 }z_i=Wx_i+b\text{,则 mini-batch 的均值 }\mu_B=\frac{1}{m}\sum(Wx_i+b)=\frac{1}{m}\sum Wx_i+b\mathrm{}\\&\bullet\quad\text{归一化时,}z_i-\mu_B=(Wx_i+b)-(\frac{1}{m}\sum Wx_i+b)=Wx_i-\frac{1}{m}\sum Wx_i\mathrm{}\\&\bullet\quad\text{关键点:这里的 }b\text{ 被完全减掉了!归一化过程尚除了输入中的任何常量偏移,包括 bias}\end{aligned}$$

2.$\beta$ 替代了 bias 的作用：

在 BN 的最后一步，输出是$y_i = \gamma \hat{x}_i + \beta$, $\beta$是一个可学习的参数，它可以自由调整输出的偏移量，完全替代了原始$b$的功能。换句话说，原始的$b$无论是什么值，都会被 BN 的均值减法抵消，而 $\beta$ 会重新学习一个合适的偏移。

3.结论：

​ 也就是说，在BN之前的bias是多余的，他在归一化的计算中被消除，由引进的$\beta$代替了其便宜调整的工作。

​ 这里需要注意的是：在训练阶段和测试阶段,BN层的工作方式是不完全一样的，Why?

之所以产生这样的差距，究其原因是因为，BN的核心计算机制是依赖于数据的统计量（均值和方差），而在训练和测试的阶段计算方式是不一样的，且听下述分析：

​ 我们知道，BN的计算公式为：

$$\bullet\quad\hat{x}_i=\frac{x_i-\mu_B}{\sqrt{\sigma_B^2+\epsilon}}\quad(\epsilon\text{是小常数,避免除零})$$

​ 关键的问题在于：$\mu$ 和 $sigma^2$的计算方式在训练和测试阶段不同。

​ 训练阶段：

​ 该阶段BN所依赖的统计量是基于当前mini-batch下统计量工作的。

$$\begin{aligned}&\bullet\quad\mu_{B}=\frac{1}{m}\sum_{i=1}^{m}x_{i}\text{(当前 batch 的均值)}\\&\bullet\quad\sigma_{B}^{2}=\frac{1}{m}\sum_{i=1}^{m}(x_{i}-\mu_{B})^{2}\text{(当前 batch 的方差)}\\&\bullet\quad m\text{ 是当前 batch 的大小}\end{aligned}$$

​ 每次前向传播时，均值和方差直接从当前 mini-batch 计算，反映了数据的局部分布。

​ 在每一个mini-batch的统计量计算的过程中，BN还会不断的一个全局统计变量，即维护一个移动平均的均值和方差（moving average），用于测试阶段。这些值通过指数移动平均（EMA）更新：

$$\begin{aligned}&\bullet\quad\mu_{\mathrm{moving}}=(1-\alpha)\cdot\mu_{\mathrm{moving}}+\alpha\cdot\mu_{B}\\&\bullet\quad\sigma_{\mathrm{moving}}^{2}=(1-\alpha)\cdot\sigma_{\mathrm{moving}}^{2}+\alpha\cdot\sigma_{B}^{2}\\&\bullet\quad\alpha\text{ 是动量参数(通常设为 }0.1\text{ 或更小,比如 }0.01)\text{}\end{aligned}$$

​ 测试阶段：

​ 在测试阶段，通常只是处理一个单一的样本（一张图片），无法计算batch的统计量，并且每次推理的结果不能因为输入的不同而变化，所以，统计量必须固定。因此，测试阶段所使用的统计量就是训练阶段不断更新的 全局统计变量。值得注意的是，既然测试阶段统计量是固定的就相当于BN层为一个线性变换。

​ 使用移动平均统计量：

$$\bullet\quad\text{均值:}\:\mu=\mu_{\mathrm{moving}}\:(\text{训练时保存的全局均值})\\\bullet\quad\text{方差:}\:\sigma^2=\sigma_{\mathrm{moving}}^2\:(\text{训练时保存的全局方差})$$

​ 也就是说，在测试阶段，不依赖当前输入的统计量，而是用训练过程中积累的全局 $\mu_{\text{moving}}$和 $\sigma^2_{\text{moving}}$，这两个参数值在训练的时候会被保存进权重文件中（也就是训练所得模型文件）。输出是确定性的，保证推理结果一致。

训练与测试的差异总结:

阶段	均值 ($\mu$)	方差 ($\sigma^2$)	统计量来源	作用
训练	$\mu_B$（当前 batch）	$\sigma_B^2$（当前 batch）	当前 mini-batch	局部标准化 + 正则化
测试	$\mu_{\text{moving}}$	$\sigma^2_{\text{moving}}$	全局移动平均	固定标准化，确定性输出

2.Anchor?

​ 1）What is Anchor?

​ 大模型给我的答案是：它指的是一组预定义的矩形框，具有固定的宽高比例和尺度。这些框在检测过程中作为参考，帮助模型预测目标的边界框（bounding box），Anchor 提供了一种初始猜测，模型通过学习这些框的偏移量（offset）和尺度调整，来精确预测目标的位置和大小。也就是说： Anchor（先验框） 就是一组预先设计好的一些边框，在训练的时候，将真实的边界框（groundtruth）相对于这些预设的边框的偏移量来构建训练样本。 这就相当于，预设边框先大致在可能的位置“框”出来目标，然后再在这些预设边框的基础上进行调整。简言之就是在图像上预设好的不同大小，不同长宽比的参照框。

​ YOLOV2是YOLO系列算法首次引入Anchor的概念（其概念是在Faster-RCNN的论文中提出的），具有里程碑的意义。

​ 在YOLOV1中。模型直接预测每个网格单元的边界框坐标（$x, y, w, h$）和置信度，没有预定义的框。这种方法对目标的形状和尺度适应性差，尤其对大小变化大的目标预测不准，导致召回率较低。

​ 在YOLOV2中引入了Anchor的概念，具体实现：

​ 使用 K-Means 聚类 从训练数据中自动生成 Anchor 的尺寸，而不是手动设置（Faster R-CNN 是手动定义）。

​ 每个网格单元预测 5 个 Anchor（VOC 数据集），输出包括位置偏移、尺度调整和置信度。

我阅读了Faster-RCNN的源代码，其AnchorsGenerator的定义代码如下：

def __init__(self, sizes=(128, 256, 512), aspect_ratios=(0.5, 1.0, 2.0)):
    super(AnchorsGenerator, self).__init__()

​ 可知，Faster-RCNN所要生成的Anchor 的尺寸，都是预先设计好的：尺寸（用来适应目标大小变化）分别为(128, 256, 512)，长宽比（用来使用目标形状变化）为(0.5, 1.0, 2.0)。也就是说，在每一个滑动窗口上，都会生成3*3=9个Anchor。关于Faster-RCNN的详细内容可至小破站【Faster RCNN理论合集】 学习。

​ 而对于YOLO来说，其Anchor的大小和形状则不是预先设计好的，而是引入了 K-Means 聚类 的方法，从训练数据中自动生成 Anchor 的尺寸。

下面这是论文原文：

'''
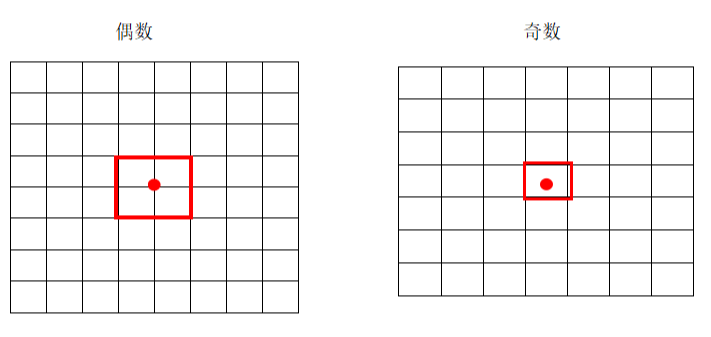
	We remove the fully connected layers from YOLO and use anchor boxes to predict
	bounding boxes. First we eliminate one pooling layer to make the output of the
	network’s convolutional layers higher resolution. We also shrink the network to
	operate on 416 input images instead of 448×448. We do this because we want an
	odd number of locations in our feature map so there is a single center cell.
	Objects, especially large objects, tend to occupy the center of the image so it’s
	good to have a single location right at the center to predict these objects instead
	of four locations that are all nearby. YOLO’s convolutional layers downsample the
	image by a factor of 32 so by using an input image of 416 we get an output
	feature map of 13 × 13.
'''

提到了相较于YOLOV1做出的改变：

​ 我们知道，YOLOv1 使用了一个类似 VGG 的网络作为backbone，包含多个卷积层和池化层，最后接上全连接层（FC）来预测边界框和类别。也就是说，多个池化层（下采样层）使特征图压缩到一个分辨率很小的情况（我记得是从448* 448->7*7），导致对小目标的检测能力不足。另外，全连接自身存在一个局限性，就是要求固定的输入尺寸，这就限制了模型对不同分辨率的适应性。，灵活性差。同时呢，FC的计算量真的太太太太大了，增加了内存和计算负担。

​ 所以上述一大串英文讲的就是，YOLOV2在YOLOV1的基础之上：

​ 删除全连接层：YOLOv2 改为全卷积网络（Fully Convolutional Network, FCN），去掉了 FC 层，直接用卷积层预测边界框和类别。

​ 移除最后一个池化层：减少下采样次数，保留更高的特征图分辨率。

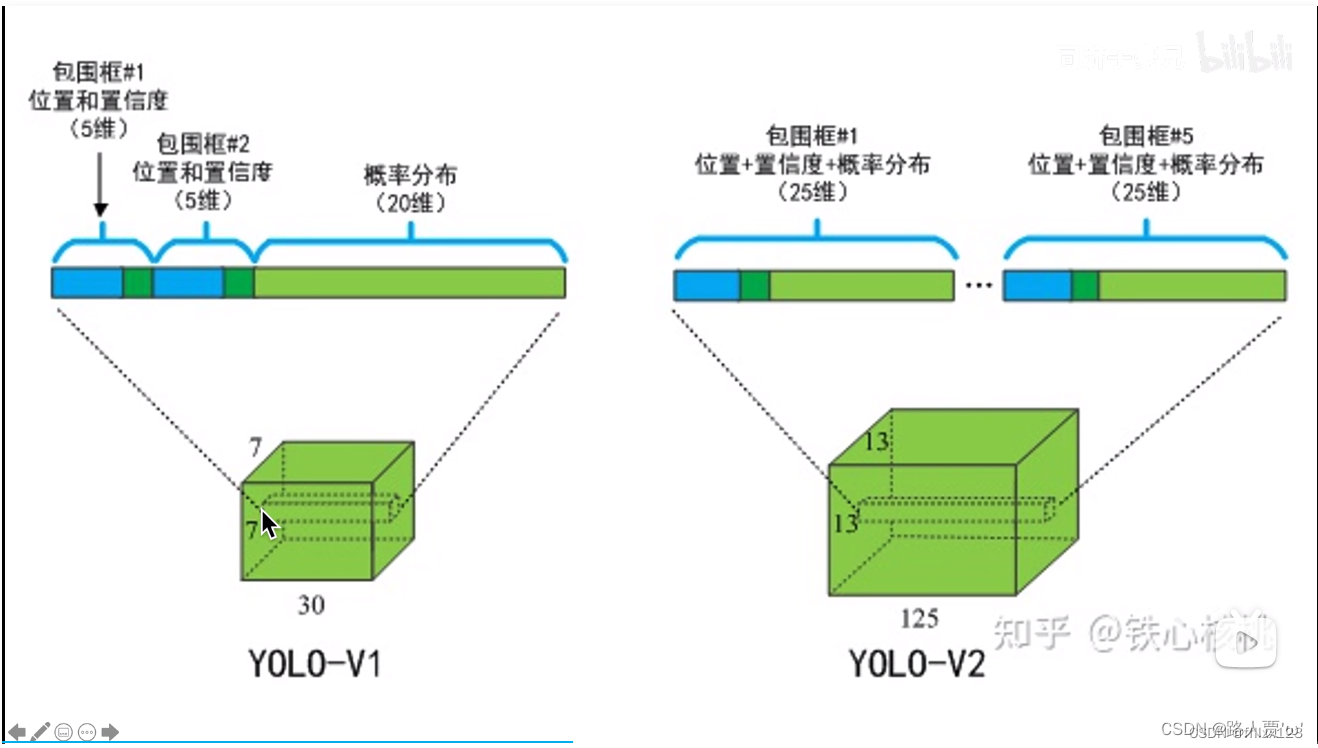
去掉了全连接层，YOLOV2的预测方式使用卷积层输出一个张量（如 $13 \times 13 \times 5 \times (5 + 20)$，其中：

​ $13\times13$ 是特征图尺寸，

​ 5 是 Anchor 数量，

​ 5+20 表示每个 Anchor 的$t_x, t_y, t_w, t_h, \text{confidence}$ 和 20 个类别概率。

为什么特征图大小为$13\times13$？

​ 因为YOLOv2 使用新的 Darknet-19 作为 backbone，包含 19 个卷积层和 5 个池化层（相比于V1少了一个池化层）。5个池化层，所以下采样倍数为：$2^5=32$。输入图片尺寸为416，那么13=416/32。 那么问题又来了，为什么输入图片尺寸是416而不是448呢？论文中也给了解释：

'''
	We do this because we want an odd number of locations in our feature map so
	there is a single center cell. Objects, especially large objects, tend to occupy the
	center of the image so it’s good to have a single location right at the center to
	predict these objects instead of four locations that are all nearby. 
'''

​ 其大概意思就是，较大的目标，其中心往往会在图像中间，那么我们希望在图像中间恰好有一个单独的位置来预测他，而不是四个。

3.How to generate anchors?

​ 使用K-Means 聚类，从训练集的真实边界框（ground truth boxes）中自动学习 Anchor 的宽高比例和尺度。过程如下：

​ 1）输入：训练数据中的所有边界框的宽高对 $(w, h)$。

​ 2）目标：聚类出$k$个簇（YOLOv2 默认$k = 5$），每个簇代表一个典型的 Anchor 尺寸。

​ 3) 距离度量：使用自定义距离函数 $d(\text{box}, \text{centroid}) = 1 - \text{IOU}(\text{box}, \text{centroid})$，而不是欧几里得距离，因为 IOU（Intersection over Union）更适合衡量边界框的匹配度。这里是自定义的IOU距离。

​ 4) 输出：$k$个 Anchor 的宽高对（如 VOC 数据集的 1.08,1.19, 3.42,4.41, …）。

​ 详细的聚类讲解可以参考这篇博文：机器学习算法----聚类 (K-Means、LVQ、GMM、DBSCAN、AGNES) (学习笔记)

​ 针对与K-means方法，需要初始簇中心（centroids），通常随机选择训练数据中的几个边界框作为初始值。这种初始值是随机的，但对最终结果影响不大，因为 K-Means 会迭代优化。一旦通过 K-Means 计算出 $k$个 Anchor 尺寸，这些值被写入配置文件,之后在训练和测试阶段，Anchor 的宽高对是固定的，不会再变化。

​ 由上可知，通过K-means方法，聚类出$5$个簇，也就是说5种尺寸大小的Anchors.即每一个grid cell预测五个boundingbox。我们知道，每一个bbox对应25的预测值，分别为 x,y,w,h 置信度(confidence)和20个类别概率。对于YOLOV2，其输出特征图大小为13*13，故需要预测13 × 13 × 5 = 845个bbox，则其输出大小为13 × 13 × 5 × 25=13 × 13 ×125。YOLOV1输出大小为：7 ×7 × 30。如下图所示：

在训练阶段和测试阶段：

​ 训练阶段：虽然 Anchor 的初始宽高是固定的，但 YOLOv2 模型并不直接使用这些值，而是通过卷积层预测每个 Anchor 的偏移量（$t_x, t_y, t_w, t_h$）和置信度，预测公式后续会提到。也就是说，训练过程就是不断预测偏移量并且调整偏移量。虽然Anchor 的初始尺寸是固定的，但通过训练，模型学会了如何使用偏移量来调整这些 Anchor 来拟合真实目标，因此最终的边界框是动态生成的。

​ 测试阶段：在推理阶段，YOLOv2 加载配置文件中的固定 Anchor 尺寸，结合预测的偏移量生成边界框。Anchor 的宽高对不会因输入图像而调整，保持 K-Means 生成的初始值。

​