YOLO源码学习过程-YOLOv2（二）

4.Some details about Dimension Clusters

​ 前文提到了YOLOv2 引入了锚框机制，希望通过预定义的锚框尺寸来更好地适应训练数据中目标的真实边界框（Ground Truth Boxes）。为了让锚框更贴合数据集，作者使用 K-Means 聚类来分析训练集中边界框的宽高分布，从而自动生成一组“先验框”（Priors）。但关键在于，聚类的目标是什么？如何定义“相似性”？

标准的K-means算法步骤：

1.随机选择K个样本作为初始簇中心
2.针对数据集中每个样本，计算它到K个初始簇中心的距离，并将其分到距离最小的聚类中心所对应的类中
3.针对每个类别，重新计算它的聚类中心
4.重复上面的步骤2、3，直到达到某个终止条件（迭代次数、最小误差变化）

​ 上面所提到的，计算每一个样本到K个初始簇中心的**距离。标准的 K-Means 聚类使用欧几里得距离**作为度量，例如对于边界框的宽高 (w, h) 和聚类中心 ($w_c, h_c$)，距离计算为：

$$d = \sqrt{(w - w_c)^2 + (h - h_c)^2}$$

​ 但是在YOLOv2中，并没有使用欧几里得距离作为度量，而是使用基于 IoU 的距离度量。Why? 论文中给出的回答是：If we use standard k-means with Euclidean distance larger boxes generate more error than smaller boxes.

​ 这个误差指的是什么？

​ 即大的边界框（例如 500x500）与聚类中心的偏差（比如差 30）产生的欧几里得距离远大于小的边界框（例如 50x50）与中心的偏差（差 10）。但实际上，对于500x500的大边界框，30的偏差可以说不是很大，但是对于50x50的边界框，10的偏差就很大了。也就是说大框的误差被放大了，而小框由于偏差较小，其误差的贡献度就小了，这是很不合理的。

​ 另外，在目标检测中，模型的最终目标是预测边界框与真实框有较高的 IoU（交并比），而不是宽高值的绝对差异。欧几里得距离只关注宽高差的数值大小，无法直接衡量两个框在空间上的重叠程度（即 IoU），因此不能很好地反映检测任务的需求。

基于 IoU 的距离度量：

​

$$d(box, centroid) = 1 - IoU(box, centroid)$$

​ $box$ 是训练集中的某个边界框

​ $centroid$ 是聚类中心（锚框的候选尺寸）

​ $IoU(box, centroid)$ 是两个框的交并比，范围在 [0, 1] 之间。

因此，$d(box, centroid)$ 的范围也是 [0, 1]，值越小表示两个框越相似。K-Means 的目标是最小化样本点到聚类中心的距离，因此用 $1 - IoU$ 将“相似性”转化为“距离”：$IoU$ 越高，距离越小，符合聚类优化的需求。并且，使用该距离作为度量，直接优化了锚框和真实框之间的匹配程度，而不仅仅是关注宽高差。

5.直接位置预测（Direct Location Prediction）

​ 回顾一下，YOLOv1的输出向量的尺寸，7x7x30，7x7为网格数量，其中30包括了20个类别概率和两个边界框的预测值。每一个边界框的预测值为：x, y, w, h和置信度（confidence）。也就是说，在YOLOv1中，每个网格单元直接预测边界框的绝对坐标。x,y为边界框的中心坐标，w,h为边界框宽度和高度。这样直接预测绝对坐标的方式，输出没有约束，可能导致预测值超出图像范围或不稳定。为了解决这些问题，YOLOv2 引入了“直接位置预测”，结合了锚框机制和相对偏移量的思想，其实也是借鉴了Faster-RCNN的思想。作者希望实现：

1.简化预测：让网络预测更直观、更稳定的参数。
2.利用先验：通过锚框提供边界框的初始猜测，网络只需微调偏移量。
3.约束输出：避免预测值超出合理范围，提高训练稳定性。

​ 直接位置预测的核心是将边界框的预测分解为“相对于锚框的偏移量”，并用 Sigmoid 函数约束中心坐标，使其保持在网格单元内部。

实现方式：

在 YOLOv2 中，每个网格单元预测 K 个锚框（K=5），每个锚框的预测包括：

• 中心坐标偏移量：$t_x, t_y$
• 宽高缩放因子：$t_w, t_h$
• 置信度（confidence）：$t_o$
• 类别概率：$P(class)$

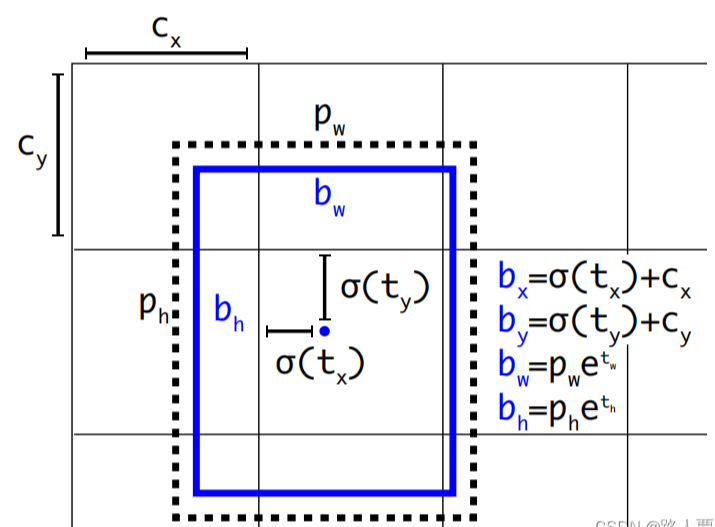
网络的输出是这些参数，然后通过变换公式计算出最终的边界框坐标 ($b_x, b_y, b_w, b_h$)。

计算公式：

$$\begin{aligned}&b_{x}=\sigma(t_{x})+c_{x}\\&b_{y}=\sigma(t_{y})+c_{y}\\&b_{w}=p_we^{t_w}\\&b_{h}=p_he^{t_h}\end{aligned}$$

$c_x,c_y$ 是 anchor box 所在的网格的左上角坐标。

$p_w,p_h$ 是先验 anchor box 的宽高（通过 K-Means 聚类生成），经过聚类之后，得到 5 个聚类中心。每个中心对应一对 $(p_w, p_h)$，即锚框的宽高。

$σ(t_x),σ(t_y)$ 表示 Sigmoid 激活函数,经过Sigmoid函数之后，数值在[0,1]之间。确保中心点位于当前网格内。

具体如何计算的，如下图所示：

​ 一个网格相对于图片左上角的偏移量就是$c_x,c_y$，所以$c_x,c_y$ 也就是 anchor box 所在的网格的左上角坐标。然后再加上预测的$b_x, b_y$这两个参数经过Sigmoid归一化之后的$σ(t_x),σ(t_y)$,就是最终的边界框的坐标 $b_x, b_y$。

​ 为什么宽高缩放指数需要经过指数函数呢？

​ 因为$t_w, t_h$是模型预测出来的，有可能为负数。边界框的宽 $b_w$ 和高 $b_h$ 必须是正值。如果直接使用$t_w$或 $t_h$（可能为负数），会导致无效的边界框。

6.Fine-Grained Features—细粒度的特征

​ YOLOv1 虽然实现了实时目标检测，但有一个明显的短板——对小目标的检测能力较弱。这是因为 YOLOv1 的特征图分辨率较低（7×7），小目标的细节信息在多次下采样后几乎丢失。YOLOv2 为了解决这个问题，引入了“精细网格（Fine-Grained Features）”机制，旨在保留更多低层特征信息，从而提升对小目标的检测能力。

​ 什么是精细网络？

​ 精细网格的核心是通过一种“Passthrough Layer”（直通层）将高分辨率的低层特征图与低分辨率的高层特征图结合。YOLOv2 的最终特征图是 13×13，但它会利用一个更高分辨率的特征图（例如 26×26），通过特殊操作将其整合到 13×13 的特征图中。

​ 说白了就是 特征融合。将低层特征图和高层特征图拼接(concat)到一起。这样就可以丰富特征表达，因为高层特征往往包含语义信息（例如目标类别）。低层特征往往包含空间细节（例如目标位置和形状）。两者的结合让模型既有全局语义，又有局部细节，适合多尺度目标检测，显著提升小目标检测能力。

具体实现方式如下图所示：图片出处：这里

​ 将26x26x512的低层特征拿出来，经过一个1x1的卷积进行降维至26x26x64，然后使用PassThroughLayer将其变为13x13x256，与高层特征13x13x1024进行拼接，得到13x13x1260的特征图。

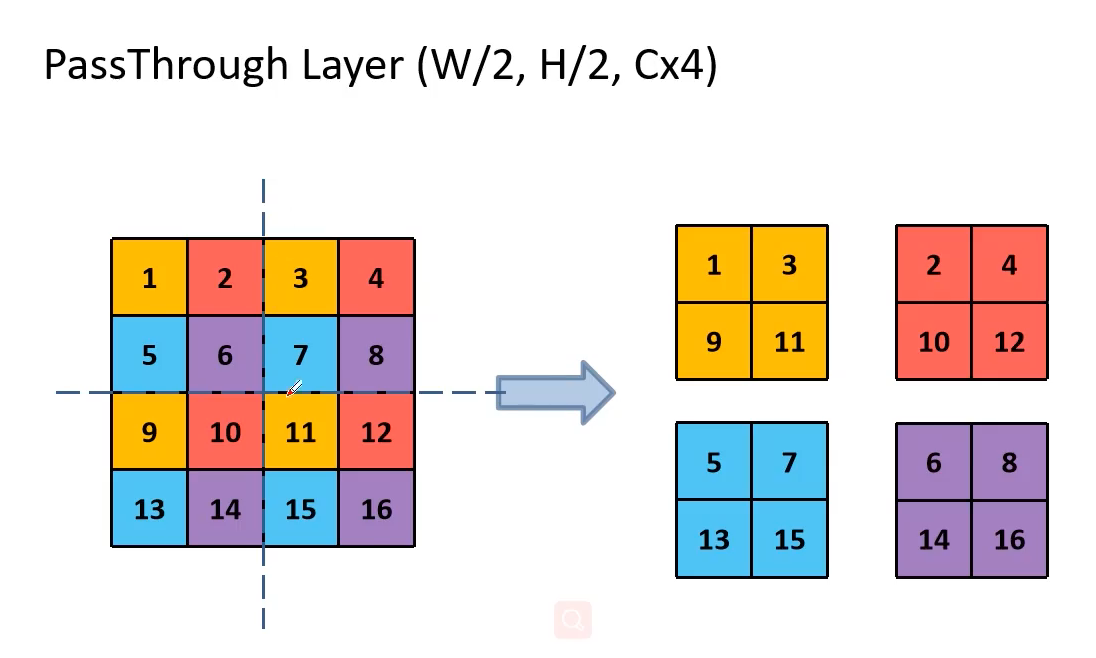
PassThroughLayer是如何工作的呢？如下图：

​ 经过PassThroughLayer之后呢，特征图的宽度和高度都变为原来的二分之一，但是维度变为原来的四倍。也就是由26x26x64变为13x13x256。

​ 上面网络结构图与原论文所表示有所不同，原论文表述中没有1x1的卷积层进行降维，但是在作者源代码的实现中，却有1x1的卷积层，这一点需要注意，作者也是留一手哈哈！

7.Multi-Scale Training—多尺度的训练

​ 首先为什么要引入多尺度训练？

​ 在目标检测任务中，目标的尺寸变化非常大。例如，在 COCO 数据集中，既有小到几十像素的物体（如小鸟），也有大到占据整张图像的物体（如汽车）。YOLOv1 固定使用 448×448 的输入分辨率，这导致模型对不同尺度的目标适应能力较弱：

​ 如果输入分辨率太低（如 320×320），小目标的细节会丢失，难以检测。

​ 如果输入分辨率太高（如 608×608），大目标检测更准，但计算量增加，推理速度变慢。

​ 多尺度训练的核心思想就是在训练过程中，周期性的改变输入图像的尺寸，让模型学习适应不同尺度的输入。这种方法使模型更具鲁棒性，既能处理小目标（高分辨率时），也能保持实时性（低分辨率时）。需要注意的是YOLOv2的输入分辨率大小必须是32的倍数，因为Darknet-19 经过 5 次最大池化（每次下采样 2 倍），总共下采样 32 倍。

实现方式：

​ 在训练过程中，每隔一定迭代（例如每 10 个 batch），随机选择一个新的分辨率。

​ 例如：

• 第 1 个 batch：输入 416×416，特征图 13×13。
• 第 11 个 batch：切换到 320×320，特征图 10×10。
• 第 21 个 batch：切换到 544×544，特征图 17×17。

​ 当网络的输入分辨率发生变化的时候，网络的输入层和输出层都要进行相应的动态调整。还需要注意的是，党对训练集图像进行调整时，其对应的标签位置信息也要进行相应的调整。

例如，原始图像 1920×1080，标注$(x, y, w, h) = (960, 540, 200, 150)$，调整到 416×416 后：

• 归一化：$x' = x \times \frac{416}{1920}$，$y' = y \times \frac{416}{1080}$，宽高同理。

不同分辨率相当于对图像进行了不同程度的缩放，类似于数据增强，防止模型过拟合单一尺度。

8.网络结构优化（Darknet-19）

​ YOLOv1 使用的骨干网络基于 GoogLeNet，包含多个 Inception 模块。虽然它实现了实时目标检测，但存在一些问题：

​ 网络参数量较大（约 6 亿次浮点运算），对硬件要求较高。

​ 检测精度（mAP）较低（例如在 VOC 2007 上约为 63.4%）。

​ 对小目标的检测能力不足，部分原因是网络下采样过多，丢失了细节信息。

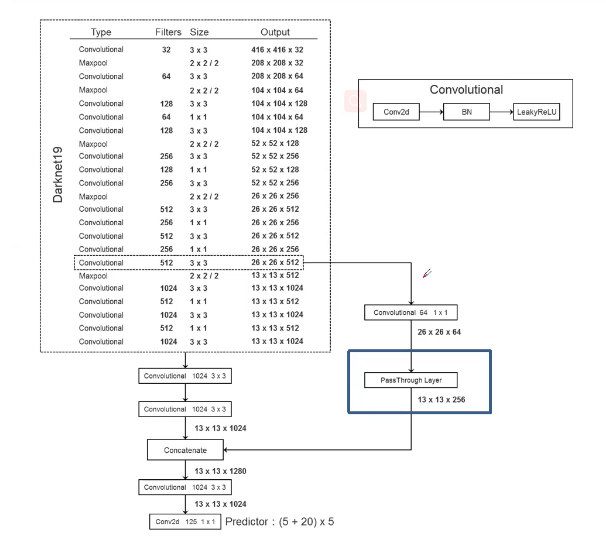
​ YOLOv2重新设计了主干网络推出了Darknet-19。这是一个更轻量化、更高效的卷积神经网络，专门为目标检测优化，既能保持实时性，又能提升检测精度。

​ Darknet-19 包含 19 层卷积层（加上激活函数和池化层，总层数更多），设计上借鉴了 VGG 和 ResNet（也就是PassThroughLayer部分） 的思想，但进行了大幅简化。

我们知道，在YOLOv1中，backbone输出特征图之后，经过了两层全连接层，将特征图重塑为 7×7×30 张量，也就是预测张量。而在YOLOv2中，完全去掉了全连接层，改用全卷积网络（Fully Convolutional Network, FCN）结构。在backbone输出特征图之后使用卷积层来输出预测张量。这样做的好处是：保留空间信息，提升检测精度。减少参数量，加快推理速度。支持多尺度输入，增强鲁棒性。

YOLOV2整体网络结构图：这里，里面的reorg层就是PassThroughLayer层。

• conv18即Darknet-19去掉分类输出3层后的最后一个卷积层。

• conv19，conv20，conv21为 3×3 的卷积层。通道数均为1024。

• reorg即论文中提到的passthrough layer。将conv13（第5个Max Pooling层之前的conv层）进行变换，再和conv20的输出进行concat后作为conv21的输入。conv13层下采样16倍，当图片输入为3×418×418时，conv15的尺寸为512×26×26，进行reorg变换后，尺寸为2048×13×13，和conv20特征图输出的大小一致。

• conv22为 1×1 的卷积层，得到预测输出的张量，生成目标框。输出的通道大小为 B×(C+5) ， B 为每个格子预测的anchor数（论文中取5）。

9.损失函数

​ 损失函数是模型优化的核心，指导网络学习如何预测边界框位置、置信度和类别。

先来回顾一下YOLOv1的损失函数：

$$\begin{aligned}\text{Loss function:}\\\lambda_{\mathrm{coord}}&\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left[\left(x_i-\hat{x}_i\right)^2+\left(y_i-\hat{y}_i\right)^2\right]\\&+\lambda_{\mathrm{coord}}\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left[\left(\sqrt{w_i}-\sqrt{\hat{w}_i}\right)^2+\left(\sqrt{h_i}-\sqrt{\hat{h}_i}\right)^2\right]\\&+\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left(C_i-\hat{C}_i\right)^2\\&+\lambda_{\mathrm{noobj}}\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{noobj}}\left(C_i-\hat{C}_i\right)^2\\&+\sum_{i=0}^{S^2}\mathbb{1}_i^{\mathrm{obj}}\sum_{c\in\mathrm{classes}}\left(p_i(c)-\hat{p}_i(c)\right)^2\end{aligned}$$

逐项来看：

$$\lambda_{\mathrm{coord}}\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left[\left(x_i-\hat{x}_i\right)^2+\left(y_i-\hat{y}_i\right)^2\right]\\+\lambda_{\mathrm{coord}}\sum_{i=0}^{S^2}\sum_{j=0}^B\mathbb{1}_{ij}^{\mathrm{obj}}\left[\left(\sqrt{w_i}-\sqrt{\hat{w}_i}\right)^2+\left(\sqrt{h_i}-\sqrt{\hat{h}_i}\right)^2\right]$$

这一部分是坐标损失（位置和尺寸），其中:

​ $1_{ij}^{obj}$ :指示变量，若第 $i$个网格的第$j$ 个边界框负责目标，则为 1，否则为 0。

​ ($x_i,y_i,w_i,h_i$)：预测的边界框坐标和宽高。

​ $(\hat{x}_i, \hat{y}_i, \hat{w}_i, \hat{h}_i)$：真实边界框的坐标和宽高。

​ $\lambda_{\text{coord}} = 5$：坐标损失的权重，强调位置重要性。

​ 使用 $\sqrt{w}$ 和 $\sqrt{h}$，因为宽高误差对小目标影响更大

$$\sum_{i=1}^{S^2}\sum_{j=1}^B1_{ij}^\mathrm{obj}(C_i-\hat{C}_i)^2+\lambda_\mathrm{noobj}\sum_{i=1}^{S^2}\sum_{j=1}^B1_{ij}^\mathrm{noobj}(C_i-\hat{C}_i)^2$$

这一部分是置信度损失，其中：

​ $Ci$：预测的置信度（目标存在概率）。

​ $\hat{C}_i$：真实置信度（IoU 与真实框的最大值）。

​ $\lambda_{\text{noobj}} = 0.5$：负样本（无目标）的置信度损失权重，平衡正负样本。

$$\sum_{i=1}^{S^2}1_i^\text{obj}\sum_{c\in\mathrm{classes}}^C(p_i(c)-\hat{p}_i(c))^2$$

这一部分是分类损失，其中：

​ $pi(c)$：预测的类别概率。

​ $\hat{p}_i(c)$：真实类别标签。

上述就是YOLOv1的损失函数，该损失函数存在那些问题呢？

​ 坐标损失直接使用平方误差，训练初期不稳定。

​ 对小目标的宽高误差未充分优化（$\sqrt{w}$ 虽有改进，但效果有限）。

​ 负样本过多（大部分网格无目标），置信度损失失衡。

​ 所以，YOLOv2以此对损失函数做出了修改，YOLOv2 引入了锚框机制（Anchor Boxes）和直接位置预测，损失函数也随之调整。假设网格大小为$S \times S$，每个网格预测 $K$ 个锚框，边界框参数为$(t_x, t_y, t_w, t_h, t_o)$，类别数为$C$。损失函数分为三部分：

坐标损失（基于偏移量和缩放因子）：

$$\begin{aligned}&L_{xy}=\sum_{i=1}^{S^2}\sum_{j=1}^K1_{ij}^\mathrm{obj}\left[(\sigma(t_x)-\sigma(t_x^*))^2+(\sigma(t_y)-\sigma(t_y^*))^2\right]\\&L_{wh}=\sum_{i=1}^{S^2}\sum_{j=1}^K1_{ij}^\mathrm{obj}\left[(t_w-t_w^*)^2+(t_h-t_h^*)^2\right]\end{aligned}$$

其中：

$$\begin{aligned}&(t_{x}^{*},t_{y}^{*})\colon\text{真实偏移量,基于网格 }c_{x},c_{y}\text{ 和真实中心 }x,y\text{ 计算}:\\&t_{x}^{*}=\frac{x}{w_{\mathrm{image}}}\cdot S-c_{x},\quad t_{y}^{*}=\frac{y}{h_{\mathrm{image}}}\cdot S-c_{y}\\&(t_{w}^{*},t_{h}^{*})\colon\text{真实缩放因子,基于描能 }p_{w},p_{h}\text{ 和真实表高 }w,h\colon\\&t_{w}^{*}=\log\left(\frac{w}{p_{w}}\right),\quad t_{h}^{*}=\log\left(\frac{h}{p_{h}}\right)\\&\sigma(t_{x}),\sigma(t_{y})\colon\text{ Sigmoid 激活,确保偏移量在 }[0,1]。\\&\text{去掉了}\sqrt{w}\text{ 和 }\sqrt{h}\text{,直接优化 }t_{w},t_{hs}\end{aligned}$$

置信度损失：

$$L_{\mathrm{obj}}=\sum_{i=1}^{S^2}\sum_{j=1}^K1_{ij}^{\mathrm{obj}}(\sigma(t_o)-1)^2+\lambda_{\mathrm{noobj}}\sum_{i=1}^{S^2}\sum_{j=1}^K1_{ij}^{\mathrm{noobj}}(\sigma(t_o)-0)^2$$

其中：

​ $\sigma(t_o)$：预测的置信度（目标存在概率）。

​ $\lambda_{\text{noobj}}$：负样本权重，通常仍为 0.5，但 YOLOv2 通过锚框机制减少了负样本数量。

分类损失：

$$L_{\mathrm{cls}}=\sum_{i=1}^{S^{2}}\sum_{j=1}^{K}1_{ij}^{\mathrm{obj}}\sum_{c=1}^{C}\left[\hat{p}_{c}\log(p_{c})+(1-\hat{p}_{c})\log(1-p_{c})\right]$$

使用交叉熵损失（YOLOv2 改进了分类损失，采用 Sigmoid 激活支持多标签）。

总损失：

$$L=\lambda_{\mathrm{coord}}(L_{xy}+L_{wh})+L_{\mathrm{obj}}+L_{\mathrm{cls}}$$

$λ_{coord}$=5 保持不变。

对比两个版本的损失：

​ 1.坐标损失的改进: YOLOv1 使用 $(x, y, \sqrt{w}, \sqrt{h})$的平方误差，YOLOv2 改为预测偏移量 $(t_x, t_y)$ 和缩放因子$(t_w, t_h$)。

​ 2.锚框机制的影响: YOLOv1 每个网格预测 2 个边界框，YOLOv2 每个网格预测 5 个锚框，损失只对 IoU 最高的锚框计算坐标损失。只优化负责目标的锚框，降低负样本干扰。

​ 3.分类损失的优化: YOLOv1 使用平方误差，YOLOv2 改为交叉熵损失，支持 Sigmoid 激活（多标签）。交叉熵更适合分类任务，收敛更快。

​ 4.负样本处理: YOLOv2 通过锚框机制减少了负样本数量，$\lambda_{\text{noobj}}$ 的作用减弱。